Penjelasan Singkat Mengenai Pointer C++

 

Pengertian Pointer

pointer merupakan variabel dengan tipe tertentu yang berguna untuk mencatat alamat dari suatu variabel yang setipe dengannya, serta mengakses, dan memanipulasi data yang tersimpan dalam alamat tersebut.

Bila int x adalah sebuah variable bertipe integer, variabel x berarti alamat dari x. Jika p adalah sebuah pointer bertipe integer, unsur p bisa menyimpan dan memegang alamat dari x tersebut.

Berdasarkan Praktikum Algoritma dan Pemrograman I oleh Sistem Informasi Universitas Dian Nusantoro, pointer adalah suatu variabel yang menunjuk kepada suatu alamat memori komputer tertentu.

Pointer ini merupakan variabel level rendah yang bisa dipakai untuk menunjuk nilai integer, character, float, double, atau single hingga tipe data lain yang didukung oleh bahasa C.

Variabel biasa mempunyai sifat statis, sedangkan pointer mempunyai sifat dinamis dan lebih fleksibel. Variabel pointer yang tak menunjuk nilai apa pun berarti mempunyai nilai NULL. Hal itu disebut sebagai dangling pointer karena nilainya tidak diinisialisasi dan tidak bisa diperkirakan.

Operator Pointer

Ada dua operator yang digunakan pada tipe data pointer yaitu:

a. Operator Deference (&)

Operator ini biasanya disebut dengan address of atau operator alamat. Dengan menggunakan operator deference (&) ini, suatu variabel akan menghasilkan alamat memori.

Contoh:

int x = 45;
cout << &x;

Pada program di atas, akan ditampilkan alamat memori dari variabel x, bukan nilai x.

b. Operator reference (*)

Operator ini biasanya disebut value pointed by. Dengan menggunakan operator ini, kita dapat mengakses secara langsung nilai yang terdapat pada suatu alamat memori.

Contoh:

int x = 45;
cout <<*&x;

Pada program di atas, akan ditampilkan nilai dari alamt memori &x.

contoh kodingan :

Output :

Mendeklarasikan Variabel Pointer

Suatu variabel pointer didefinisikan dengan bentuk sebagai berikut:

tipe_data *nama_variabel

• tipe_data dapat berupa sembarang tipe seperti halnya pada pendefinisian variabel bukan pointer.
• nama_variabel adalah nama variabel pointer.

Contoh1:

#include <iostream.h>
#include <conio.h>

void main() {
int x, y; int *px;
x = 89;
y = x;
px = &x;
cout << "Nilai x = " << x << endl;
cout << "Nilai y = " << y << endl;
cout << "Alamat px = " << px << endl;
cout << "Nilai px = " << *px << endl;

getch();
}

Output:

Nilai x = 89
Nilai y = 89
Alamat px = 0×0012ff88
Nilai px = 89

Pointer Pada Pointer

Tidak terbatas menunjuk alamat dari suatu variabel, pointer dapat pula menunjuk ke pointer lainnya. Dalam pendeklarasiannya, kita tambahkan pointer reference (*) pada variabel yang akan ditunjuk.

Contoh:

int x;
int *px; //pointer ke variabel int
**ppx; //pointer pada pointer

x = 100;
px = &nama;
ppx = &pNama;

Contoh Program:

#include <iostream.h>
#include <conio.h>

void main() {
int x;
int *px; //pointer ke variabel
int **ppx; //pointer ke pointer

x = 175;
px = &x;
ppx = &px;
cout << "Nilai x = " << x << endl;
cout << "Nilai px = " << *px << endl;
cout << "Nilai ppx = " << **ppx << endl;

getch();
}

Output:

Nilai x = 175
Nilai px = 175
Nilai ppx = 0×0012ff88

 Pointer Pada Array

Pada Array/Larik, pointer hanya perlu menunjukan alamat elemen pertama saja karena alamat array dalam memori sudah disusun secara berurutan.

Contoh:

int a[] = {76, 67, 88, 98};
int *pa;
pa = a;

Pernyataan pa=a artinya pointer pa menyimpan alamat array a, yang alamatnya diwakili alamat elemen pertama, yaitu a[0]. Kita juga bisa mengganti perintah pa=a dengan pa=&a[0]. Untuk pembacaan semua elemen array dengan pointer, bisa menggunakan perulangan seperti pada penggalan program berikut.

for (int i=0; i < 4; i++) {
cout << *pa << " ";
pa++;
}

Contoh Program:

#include <iostream.h>
#include <conio.h>
#define MAX 5

void main() {
int a[MAX];
int *pa; pa = a; //atau pa = &a[0]

for (int i = 0; i < MAX; i++) {
cout << "Masukkan Nilai " << i+1 << " : ";
cin >> a[i];
}

cout << endl;

for (int i = 0; i < MAX; i++) {
cout << "Nilai a[" << i << "] = " << *pa << endl;
pa++;
}

getch();
}

Output:

Masukkan Nilai 1 : 100
Masukkan Nilai 2 : 120
Masukkan Nilai 3 : 50
Masukkan Nilai 4 : 111
Masukkan Nilai 5 : 47

Nilai a[0] = 100
Nilai a[1] = 120
Nilai a[2] = 50
Nilai a[3] = 111
Nilai a[4] = 47

 Pointer pada String

Pointer pada string dapat anda lihat pada contoh program berikut:

#include <iostream.h>
#include <conio.h>
#define MAX 5

void main() {
char nama[] = "Albert Einstein";
char *pNama = nama;

cout << "Nama = " << nama << endl;
cout << "pNama = " << pNama << endl;
pNama += 7; cout << "\nSetelah pNama += 7" << endl;
cout << "Nama = " << nama << endl;
cout << "pNama = " << pNama << endl;

getch();
}

Output:

Nama = Albert Einstein
pNama = Albert Einstein

Setelah pNama += 7
Nama = Albert Einstein
pNama = Einstein

Fungsi Rekursif Pada C++

 Pengertian Rekursif 

Rekursif adalah suatu proses dari sebuah fungsi yang dapat memanggil dirinya sendiri secara berulang-ulang. Berbeda dengan fungsi atau prosedur yang mana keduanya hanya bisa dilakukan pemanggilan dari fungsi atau prosedur lain, sementara rekursif dapat memanggil fungsinya sendiri. Jadi fungsi rekursif c++ ini akan berjalan dengan melakukan proses sampai sebuah kondisi yang ditetapkan pada fungsi tersebut terpenuhi.

Fungsi rekursif adalah salah satu teknik pemrograman yang cukup penting, dimana dalam beberapa kasus menggunakan fungsi rekursif akan jauh lebih mudah. Selain itu proses yang berjalan akan jauh lebih cepat dan efisien, hanya saja akan membutuhkan space memori yang cukup banyak karena proses iterasi dari bagian fungsi tersebut akan dipanggil secara terus menerus sehingga memerlukan ruang penyimpanan yang cukup besar jika dibandingkan dengan proses lainnya.

Bahasa pemrograman C++ mendukung penggunaan rekursif. Penerapan fungsi ini juga cukup banyak, yang paling sering misalnya untuk mencari nilai pangkat dan menghitung nilai faktorial. Kali ini saya akan membagikan kepada teman-teman bagaimana contoh penerapan fungsi rekrursif pada C++ melalui 2 contoh sederhana berikut:

Menghitung Nilai Faktorial Dengan Rekursif

#include <iostream>
using namespace std;

long int faktorial (int A);

int main(){
	
	int r,hasil;
	
	cout<<"MENGHITUNG NILAI FAKTORIAL DENGAN REKURSIF"<<endl;
	cout<<endl;
	cout<<"Masukan Nilai = ";
	cin>>r;
	
	hasil=faktorial(r);
	cout<<"Faktorial "<<r<<"!= "<<hasil<<endl;
}

long int faktorial (int A){
	if (A==1)
		return(A);
		else
		return (A*faktorial(A-1));
}

Pada contoh yang pertama kita akan mencari nilai faktorial dari nilai yang dimasukan oleh pengguna, Program diatas saya membuatnya lewat aplikasi Dev C++. Header yang saya gunakan hanya iostream terkait input/ouput ada program, Karena jenis program yang saya buat adalah program sekuensial maka saya perlu inisialisasi fungsi rekursifnya di awal sebelum fungsi main(). Pada fungsi main pengguna akan memasukan nilai dan disimpan pada variabel r nantinya akan dipanggil fungsi faktorial() dengan nilai parameter yang dibawah adalah nilai r tersebut, lalu kemudian disimpan pada variabel hasil.

Coba perhatikan pada fungsi rekursif-nya:

long int faktorial (int A){
  if (A==1)
	return(A);
	else
	return (A*faktorial(A-1));
}

Disini kita membuat fungsi rekursif dimana jika nilai yang dimasukan adalah 1 maka nilai balik (return value) adalah nilai itu sendiri. Sementara jika tidak maka akan dihitung menggunakan rumus faktorial yaitu (A*faktorial(A-1)).

Hasil Output:

Fungsi Rekursif Untuk Menghitung Pangkat

#include <iostream>
using namespace std;

long int pangkatrekursif(int x, int y);

int main(){
	
	int x,y;
	
	cout<<"FUNGSI REKURSIF UNTUK MENGHITUNG PANGKAT"<<endl;
	cout<<endl;
	cout<<"Masukan Nilai X = ";
	cin>>x;
	
	cout<<"Masukan Nilai Y = ";
	cin>>y;
	cout<<endl;
	cout<<x<<" Dipangkatkan "<<y<<" = "<<pangkatrekursif(x,y)<<endl;
}


long int pangkatrekursif(int x, int y){
	 if (y==0)
		 return 1 ;
		 else 
                 return x * pangkatrekursif(x,y-1);
} 

Pada contoh fungsi rekursif c++ yang kedua adalah untuk menghitung pangkat. Pengguna akan memasuka nilai x dan y lalu kemudian nilai x angkat dipangkatkan dengan nilai y.

Jika kita lihat pada fungsi rekursif-nya:

long int pangkatrekursif(int x, int y){
  if (y==0)
	return 1 ;
	else 
        return x * pangkatrekursif(x,y-1);
 } 

disini kita membuat fungsi dengan nama pangkatrekursif dengan menggunakan 2 parameter yaitu nilai x dan y, jika nilai y yang dimasukan adalah 0 maka akan di set nilai baliknya adalah 1, namun jika tidak maka fungsi tersebut di set nilai baliknya dimana nilai x akan dikalikan nilai y-1.

Hasil Output :

Kesimpulan Pada Materi Rekursif  :

Demikian pembahasan kali ini mengenai contoh fungsi rekursif di C++, Dari contoh yang sudah kita bahas diatas dapat saya simpulkan bahwa fungsi rekursif memungkinkan untuk dapat memanggil dirinya sendiri, Rekursif dapat menyelesaikan persoalan terkait iterasi namun diperlukan pendefinisian yang jelas untuk menentukan keadaan iterasi tersebut berhenti.

Sorting pada C++

 Pengertian Sorting

 Sorting  adalah Salah satu bagian penting dari struktur data pada proses pengurutan data. Data terkadang akan berada dalam bentuk yang tidak berpola ataupun dengan pola tertentu yang tidak kita inginkan. Namun dalam penggunaannya, kita akan selalu ingin menggunakan data tersebut dalam bentuk yang rapi atau berpola sesuai dengan yang kita inginkan. Maka dari itu proses sorting adalah proses yang sangat penting dalam struktur data. Proses pengurutan banyak ditemukan dalam pemrosesan komputer. Data yang sudah terurut memiliki beberapa keuntungan. Selain mempercepat pencarian, data yang sudah terurut juga dapat dengan mudah menentukan Nilai terbesar atau terkecil.

Pengurutan data memang sangat relevan dan merupakan aktivitas yang sangat penting berkaitan dengan pemrosesan data. Bahkan pengurutan data telah banyak dilakukan dengan bantuan alat. Adanya kebutuhan terhadap peroses pengurutan memunculkan bermacam-macam metode pengurutan yang bertujuan untuk memperoleh metode pengurutan yang optimal.

Beberapa metode yang dapat digunakan untuk pengurutan antara lain:

1. Bubble Sort
2. Selection Sort
3. Quick Sort
4. Merge Sort
5. Heap Sort
6. Shell Sort
7. Radix Sort
8. Tree Sort
9. Maximum Sort
10. Insertion Sort

Banyaknya metode pengurutan yang tersedia menimbulkan pertanyaan: algoritma manakah yang memiliki kinerja yang baik? Kinerja pengurutan data sangat menentukan kinerja sistem, karena itu pemilihan metode pengurutan yang cocok akan berperan dalam suatu aplikasi. Metode pengurutan yang akan dibahas adalah metode pengurutan Bubble Sort, Quick Sort, Maximum/Minimum Sort, Shell Sort, Merge Sort, dan Insertion.

Bubble Sort

Bubble Sort adalah metode yang membandingkan elemen yang sekarang dengan elemen-elemen berikutnya. Pembandingan elemen dapat dimulai dari awal atau mulai dari paling akhir. Apabila elemen yang sekarang lebih besar (untuk urut menaik) atau lebih kecil (untuk urut menaik) dari elemen berikutnya, maka posisinya ditukar, tetapi jika tidak maka posisinya tetap.

Contoh : Misalkan kita mempunyai array Nilai sebanyak 8 elemen akan diurutkan secara menaik dengan metode Bubble Sort: 25, 71, 30, 45, 20, 15, 6, 50.

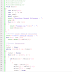
contoh kodingan :

#include<iostream.h>

#include<conio.h>

#include<iomanip.h>

void main()

{

int Nilai[20];

int i, j, k, N;

int temp;

bool tukar;

cout<<"Masukkan Banyak Bilangan : ";

cin>>N;

for(i=0; i<N; i++)

{

cout<<"Elemen ke-"<<i<<" : ";

cin>>Nilai[i];

}

}

//Proses Cetak Sebelum diurutkan

cout<<"\nData sebelum diurut : ";

for(i=0; i<N; i++)

cout<<setw(3)<<Nilai[i];

//Proses Pengurutan

i=0;

tukar = true;

while ((i<=N-2) && (tukar))

{

tukar = false;

for(j=N-1; j>=i+1; j--)

{

if(Nilai[j] < Nilai[j-1])

{

{

temp = Nilai[j];

Nilai[j] = Nilai[j-1];

Nilai[j-1] = temp;

tukar = true;

cout<<"\nUntuk j = " <<j<<" : ";

for(k=0; k<N; k++)

cout<<set(3)<<Nilai[k];

}

}

i++;

}

//Proses Cetak Setelah diurutkan

cout<<"\nData Setelah di urut : ";

for(i=0; i<N; i++)

cout<<setw(3)<<Nilai[i];

getch();

}

Quick Sort

Quick Sort merupakan metode tercepat dalam proses pengurutan data dengan menggunakan prinsip rekursif. Metode ini menggunakan strategi “pecah-belah” dengan mekanisme berikut ini.

Misalkan kita mempunyai array Nilai[k..l]. Array dipartisi menjadi dua bagian array kiri Nilai[k..m] dan array kanan Nilai[m+1..l]. Dasar mempartisi array menjadi dua adalah dengan mengambil elemen pertama sebagai elemen pivot. Letakkan semua elemen array yang lebih kecil dari pivot ke sebelah pivot dan semua elemen array yang lebih besar dari pivot ke sebelah kanan pivot. Elemen-elemen yang di sebelah kiri elemen pivot merupakan elemen-elemen array Nilai[k..m] sedangkan elemen-elemen array Nilai[m+2..l] adalah semua elemen yang lebih besar dari pivot. Lakukan hal yang sama seperti di atas terhadap array Nilai[k..m] dan Nilai[m+1..l] hingga tidak dapat dipartisi lagi.

Contoh: Misalkan kita mempunyai array Nilai sebanyak 8 elemen akan diurutkan secara menaik dengan metode Maximum Sort: 25, 72, 30, 45, 20, 15, 6, 50. Urutan langkah pengurutannya seperti berikut dan programnya dapat dilihat pada program ini.

contoh kodingan :

/* Program Pengurutan Metode Quick Sort

Pengurutan Secara Menaik

Nama File : Lat_Sorting_02a */

#include<iostream.h>

#include<conio.h>

#include<iomanip.h>

void Cetak(int data[], int n)

{

int i;

for(i=0; i<n; i++)

cout<<setw(3)<<data[i];

cout<<"\n";

}

int Partisi(int data[], int p, int r)

{

int x, i, j, temp;

x = data[p];

i=p;

j=r;

while(l)

{

while(data[j]>x)

j--;

while(data[i]<x)

i++;

if(i<j)

{

temp = data[i];

data[i] = data[j];

data[j] = temp;

}

else

return j;

}

}

void Quick_Sort(int data[], int p, int r)

{

int q;

if(p<r)

{

q=Partisi(data, p, r+1);

Quick_Sort(data, p, 1);

Quick_Sort(data, q+1, r);

}

}

void main()

{

int Nilai[20];

int i, N;

cout<<"Masukkan Banyak Bilangan : ";

cin>>N;

for(i=0; i<N; i++)

{

cout<<"Elemen ke-"<<i<<" : ";

cin>>Nilai[i];

}

cout<<"\nData Sebelum di urut : ";

Cetak(Nilai, N);

cout<<endl;

Quick_Sort(Nilai, 0, N-1);

cout<<"\nData Setelah di urut : ";

Cetak(Nilai,N);

getch();

}

Metode Maximum/Minimum Sort

Metode Maximum/Minimum Sort dilakukan berdasarkan pemilihan elemen maksimum/minimum, maka metode ini disebut juga dengan metode pemilihan/seleksi (Selection Sort).

 Metode Maximum Sort

Metode ini disebut dengan metode Maximum karena didasarkan pada pemilihan elemen maksimum sebagai dasar pengurutan. Konsepnya adalah memilih elemen maksimum kemudian mempertukarkan elemen maksimum tersebut dengan elemen paling akhir untuk urut menaik dan elemen pertama untuk urut menurun. Selanjutnya elemen paling akhir/awal tersebut di-“isolasi”, artinya elemen tersebut tidak disertakan lagi untuk tahapan berikutnya. Proses yang sama dilakukan kembali terhadap elemen array yang tersisa, yaitu memilih elemen maksimum kemudian mempertukarkan elemen maksimum tersebut dengan elemen paling akhir/awal dari array yang tersisa tadi. Kemudian diisolasi kembali. Demikian seterusnya hingga semua elemen terurut.

Contoh: Misalkan kita mempunyai array Nilai sebanyak 8 elemen akan diurutkan secara menaik dengan metode Maximum Sort: 25, 72, 30, 45, 20, 15, 6, 50. Urutan langkah pengurutannya seperti berikut dan programnya dapat dilihat pada program ini.

/* Program Pengurutan Metode Maximum Sort

*/

#include<iostream.h>

#include<conio.h>

#include<iomanip.h>

void main()

{

int Nilai[20];

int i, j, N, l;

int temp, U, Imaks;

cout<<"Masukkan Banyak Bilangan : ";

cin>>N;

for(i=0; i<N; i++)

{

cout<<"Elemen ke-"<<i<<" : ";

cin>>Nilai[i];

}

//Proses Cetak Sebelum diurutkan

cout<<"\nData sebelum diurut : ";

for(i=0; i<N; i++)

cout<<setw(3)<<Nilai[i];

//Proses Pengurutan

U=N-1;

for(i=0; i<=N-2; i++)

{

Imaks = 0;

for(j=1; j<=U; j++)

{

if(Nilai[j] > Nilai[Imaks])

Imaks = j;

}

temp = Nilai[U];

Nilai[U] = Nilai[Imaks];

Nilai[Imaks] = temp;

U--;

cout<<endl;

for(l=0; l<N; l++)

cout<<setw(3)<<Nilai[l];

}

cout<<"\nData Setelah di urut : ";

for(i=0; i<N; i++)

cout<<setw(3)<<Nilai[i];

getch();

}

Metode Minimum Sort

Metode ini disebut dengan metode minimum karena didasarkan pada pemilihan elemen minimum sebagai dasar pengurutan. Konsepnya adalah memilih elemen minimum kemudian mempertukarkan elemen minimum tersebut dengan elemen paling akhir untuk urut menaik dan elemen pertama untuk urut menurun. Selanjutnya elemen paling akhir/pertama tersebut di “isolasi” artinya elemen tersebut tidak disertakan lagi untuk tahapan berikutnya. Proses yang sama dilakukan kembali terhadap elemen array yang tersisa, yaitu memilih elemen minimum kemudian mempertukarkan elemen minimum tersebut dengan elemen paling akhir/pertama dari array yang tersisa tadi. Kemudian diisolasi kembali. Demikian seterusnya hingga semua elemen terurut.

Contoh: Misalkan kita mempunyai array Nilai sebanyak 8 elemen akan diurutkan secara menaik dengan metode Minimum Sort: 25, 72, 30, 45, 20, 15, 6, 50. Urutan langkah pengurutannya seperti berikut dan programnya dapat dilihat pada program ini.

/* Program Pengurutan Metode Minimum Sort

*/

#include<iostream.h>

#include<conio.h>

#include<iomanip.h>

void main()

{

int Nilai[20];

int i, j, N, l;

int temp, Imin;

cout<<"Masukkan Banyak Bilangan : ";

cin>>N;

for(i=0; i<N; i++)

{

cout<<"Elemen ke-"<<i<<" : ";

cin>>Nilai[i];

}

//Proses Cetak Sebelum diurutkan

cout<<"\nData sebelum diurut : ";

for(i=0; i<N; i++)

cout<<setw(3)<<Nilai[i];

//Proses Pengurutan

for(i=0; i<=N-2; i++)

{

Imin = i;

for(j=i+1; j<N; j++)

{

if(Nilai[j] < Nilai[Imin]);

Imin = j;

}

temp = Nilai[i];

Nilai[i] = Nilai[Imin];

Nilai[Imin] = temp;

cout<<endl;

for(l=0; l<N; l++)

cout<<setw(3)<<Nilai(l);

}

cout<<"\nData Setelah di urut : ";

for(i=0; i<N; i++)

cout<<setw(3)<<Nilai[i];

getch();

}

Metode Shell Sort

Metode ini dinamakan sesuai dengan penciptanya, yaitu D.L. Shell. Metode ini mirip dengan metode Bubble Sort, hanya saja perbandingan dilakukan bukan antara dua bilangan yang berurutan, akan tetapi antara dua bilangan dengan jarak tertentu. Jarak ditentukan dengan N Div 2, dimana N adalah banyaknya elemen array. Lakukan pertukaran tempat jika setiap kali perbandingan dipenuhi (lebih besar untuk urut menaik dan lebih kecil untuk urut menurun). Setiap kali perbandingan terhadap keseluruhan elemen selesai dilakukan, maka perbandingan yang baru dilakukan kembali dimana jarak diperoleh dengan Jarak Div 2 (jarak diperoleh dari Nilai jarak sebelumnya). Perbandingan keseluruhan dilakukan sampai Nilai jarak sama dengan 1 (satu). Pada saat jarak berNilai 1, maka metode Shell Sort sama dengan metode Bubble Sort.

Contoh: Misalkan kita mempunyai array Nilai sebanyak 8 elemen akan diurutkan secara menaik dengan metode Shell Sort: 25, 72, 30, 45, 20, 15, 6, 59. Urutan langkah pengurutannya seperti berikut.

contoh kodingan :

/* Program Pengurutan Metode Shell Sort

*/

#include<iostream.h>

#include<conio.h>

#include<iomanip.h>

void main()

{

int Nilai[20];

int i, N, l, k;

int temp, jarak, s;

cout<<"Masukkan Banyak Bilangan : ";

cin>>N;

for(i=0; i<N; i++)

{

cout<<"Elemen ke-"<<i<<" : ";

cin>>Nilai[i];

}

//Proses Cetak Sebelum diurutkan

cout<<"\nData sebelum diurut : ";

for(i=0; i<N; i++)

cout<<setw(4)<<Nilai[i];

//Proses Pengurutan

jarak = N / 2;

cout<<"\nJarak = "<<jarak;

while(jarak >=1)

{

do

{

s=0;

for(i=0; i<=(N-jarak)-1; i++)

{

k=i+jarak;

if(Nilai[i] > Nilai[k])

{

temp = Nilai[i];

Nilai[i] = Nilai[k];

Nilai[k] = temp;

s=1;

for(l=0; l<N; l++)

cout<<setw(4)<<Nilai[i];

cout<<"\n\t";

getch();

}

}

}

while(s!=0);

jarak /= 2;

cout<<"\nJarak= "<<jarak;

}

cout<<"\nData Setelah di urut : ";

for(i=0; i<N; i++)

cout<<setw(4)<<Nilai[i];

getch();

Metode Merge Sort

Metode ini memanfaatkan keteraturan yang diperoleh dari hasil merging dua buah array. Suatu array Nilai yang mempunyai N elemen (Nilai[0..N-1]) dianggap terdiri dari N array yang masing-masing terdiri dari satu elemen. Untuk pasangan array yang berdekatan kita lakukan merging sehingga diperoleh N/2 buah array yang masing-masing array memiliki 2 elemen (jika N ganjil, akan terdapat sebuah array dengan 1 elemen). Pada saat melakukan proses merging dilakukan pengaturan posisi dengan cara elemen yang lebih kecil diletakkan di posisi awal (untuk pengurutan secara menaik) dan elemen yang lebih besar diletakkan di posisi awal(untuk pengurutan secara menurun). Kemudian dilakukan merging kembali untuk setiap pasanga array seperti cara di atas sehingga kita peroleh N/2 buah array yang masing-masing array memiliki 4 elemen. Langkah ini kita teruskan hingga kita memperoleh sebuah array yang sudah dalam keadaan terurut.

Metode Insertion Sort

Metode Insertion Sort merupakan metode pengurutan dengan cara menyisipkan elemen array pada posisi yang tepat. Pencarian yang tepat dilakukan dengan melakukan pencarian beruntun di dalam array. Selama pencarian posisi yang tepat dilakukan pergeseran elemen array. Algoritma pengurutan ini tepat untuk persoalan menyisipkan elemen baru ke dalam array yang sudah terurut. Misalnya dalam permainan kartu, kartu yang dicabut biasanya disisipkan oleh pemain pada posisi yang tepat sehingga penambahan kartu tersebut membuat semua kartu tetap terurut.

Misalkan kita memiliki suatu array dengan N maka pengurutan secara menaik dengan metode Insertion Sort sebagai berikut:

Langkah -1: elemen pertama Nilai[0] diasumsikan telah sesuai tempatnya.

Langkah -2: ambil elemen ke dua (Nilai[1]), cari lokasi yang tepat pada Nilai[0..0] untuk Nilai Nilai[1]. Lakukan pergeseran ke kanan jika Nilai[0..1] lebih besar (untuk urut menaik) atau lebih kecil (untuk urut menurun) dari Nilai[1]. Misalnya posisi yang tepat adalah j, maka sisipkanlah Nilai[1] pada Nilai[j].

Langkah -3: ambil elemen ke tiga (Nilai[2]), cari lokasi yang tepat pada Nilai[0..1] untuk Nilai[2]. Lakukan pergeseran ke kanan jika Nilai[0..2] lebih besar (untuk urut menaik) atau lebih kecil (untuk urut menurun) dari Nilai[2]. Misalnya posisi yang tepat adalah j, maka sisipkanlah Nilai[2] pada Nilai[j].

Langkah -4: ambil elemen ke empat (Nilai[3]), cari lokasi yang tepat pada Nilai[0..3] untuk Nilai Nilai[3]. Lakukan pergeseran ke kanan jika Nilai[0..2] lebih besar (untuk urut menaik) atau lebih kecil (untuk urut menurun) dari Nilai[3]. Misalnya posisi yang tepat adalah j, maka sisipkanlah Nilai[3] pada Nilai[j].

…

Langkah –N: ambil elemen ke N (Nilai[N]), cari lokasi yang tepat pada Nilai[0..N-1] untuk Nilai Nilai[N]. Lakukan pergeseran ke kanan jika Nilai[0..N-1] lebih besar (untuk urut menaik) atau lebih kecil (untuk urut menurun) dari Nilai[N]. Misalnya posisi yang tepat adalah j, maka sisipkanlah Nilai[N] pada Nilai[j].

Contoh: Misalkan kita mempunyai array Nilai sebanyak 8 elemen akan diurutkan secara menaik dengan metode Insertion Sort: 25, 72, 30, 45, 20, 15, 6, 50. Urutan langkah pengurutannya seperti berikut:

contoh kodingan:

/* Program Pengurutan Metode Insertion Sort

*/

#include<iostream.h>

#include<conio.h>

#include<iomanip.h>

void main()

{

int Nilai[20];

int i, j, k, N;

int temp;

cout<<"Masukkan Banyak Bilangan : ";

cin>>N;

for(i=0; i<N; i++)

{

cout<<"Elemen ke-"<<i<<" : ";

cin>>Nilai[i];

}

//Proses Cetak sebelum diurutkan

cout<<"\nData sebelum diurut : ";

for(i=0; i<N; i++)

cout<<setw(3)<<Nilai[i];

//Proses Pengurutan

for(i=1; i<N; i++)

{

temp = Nilai[i];

j=i-1;

while((temp <= Nilai(j)) && (j>=1))

{

Nilai[j+1] = Nilai[j];

j--;

}

if(temp >= Nilai[j])

Nilai[j+1] = temp;

else

{

Nilai[j+1] = Nilai[j];

Nilai[j] = temp;

}

cout<<endl;

for(k=0; k<N; k++)

cout<<setw(3)<<Nilai[k];

}

//Proses Cetak Setelah diurutkan

cout<<"\nData Setelah di urut : ";

for(i=0; i<N; i++)

cout<<setw(3)<<Nilai[i];

getch();

}